Mục tiêu của Machine Learning là tìm ra các phần tử trong dữ liệu và sử dụng các phần tử đó để đưa ra dự đoán. Nó cũng có thể cung cấp cho chúng ta một framework để thảo luận về các vấn đề và giải pháp Machine Learning – như bạn sẽ thấy trong bài viết này.
Đầu tiên, chúng ta sẽ bắt đầu với các định nghĩa và ứng dụng của Machine Learning. Sau đó, chúng ta sẽ thảo luận về sự trừu tượng (Abstraction) trong Machine Learning và sử dụng điều đó để tổng kết nội dung thảo luận: dữ liệu, mô hình, mô hình tối ưu hóa và thuật toán tối ưu hóa. Sau đó trong bài viết, chúng ta sẽ thảo luận về các chủ đề cơ bản với vai trò nền tảng cho tất cả các phương pháp Machine Learning, và tổng kết lại với hướng dẫn thực hành sử dụng Machine Learning. Cuối cùng, là cách nâng cao thực hành và nghiên cứu về Machine Learning.
Hãy bắt đầu nào.

Vậy, chính xác thì Machine Learning là gì?
Khái niệm về Machine Learning
Machine Learning nói chung là một tập hợp các kỹ thuật để tìm các phần tử trong dữ liệu. Các ứng dụng của Machine Learning bao gồm từ xe tự lái thông minh, trợ lý cá nhân AI, phát minh sáng kiến chuyển thể thành giọng nói và văn bản dịch từ tiếng Pháp và tiếng Đài Loan. Ngoài ra, có một vài ứng dụng phổ biến của Machine Learning đã hoặc có khả năng ứng dụng vào quảng cáo Google hoặc những công việc hàng ngày của một doanh nghiệp như sau:
- Phát hiện lạ thường
Nhận biết các đột biến trong lưu lượng truy cập Website hoặc hoạt động ngân hàng có điều bất thường.
- Đề xuất nội dung tương tự
Tìm sản phẩm bạn có thể đang tìm kiếm hoặc thậm chí các bài viết trên Website có liên quan.
- Tiên liệu tương lai
Lập kế hoạch lộ trình của các phương tiện công cụ có liên quan hoặc xác định và ngoại suy xu hướng thị trường cổ phiếu.
Mục tiêu và cơ sở của Machine Learning
Trên đây là một vài trong số nhiều ứng dụng của Machine Learning, nhưng hầu hết các ứng dụng đều liên quan đến việc phân bổ dữ liệu cơ bản. Sự phân bổ chỉ định các sự kiện và xác suất của từng sự kiện. Ví dụ:
- Với xác suất 50%, bạn mua một mặt hàng 5 đô la trở xuống.
- Với xác suất 25%, bạn mua một món hàng 5 – 10 đô la.
- Với xác suất 24%, bạn mua một mặt hàng 10 – 100 đô la.
- Với xác suất 1%, bạn mua một mặt hàng > 100 đô la.
Với cách phân bổ này, chúng ta có thể hoàn thành tất cả các nhiệm vụ ở trên. Ví dụ:
- Phát hiện dị thường
Với 100 đô la mua hàng, chúng ta có thể chắc chắn gọi đây là sự bất thường.
- Đề xuất nội dung tương tự
Mua 3 đô la có nghĩa là chúng ta nên đề xuất nhiều mặt hàng hơn từ 5 đô la trở xuống.
- Tiên liệu tương lai
Nếu không có bất kỳ thông tin trước, chúng ta có thể dự đoán rằng lần mua tiếp theo sẽ là 5 đô la trở xuống.
Với việc phân phối dữ liệu, chúng ta có thể hoàn thành vô số nhiệm vụ. Tóm lại, một trong số các mục tiêu của Machine Learning là học cách phân bổ này.
Thậm chí tổng quát hơn, mục tiêu của chúng ta là tìm hiểu một chức năng cụ thể với Input và Output (đầu vào và đầu ra) cụ thể. Chúng ta gọi chức năng này là model (phương trình) của chúng ta. Input được ký hiệu là x. Với mô hình này, chấp nhận Input x, được hàm là: f(x) = ax
Ở đây, a là một parameter (tham số) của mô hình. Mỗi tham số tương ứng với một ví dụ khác nhau. Nói cách khác, phương trình a = 2 khác với phương trình a = 3. Trong Machine Learning, mục tiêu của chúng ta là tìm hiểu thông số này, thay đổi nó cho đến khi chúng ta làm “tốt”. Vậy làm thế nào để xác định những giá trị nào của a là “tốt”?
Chúng ta cần xác định cách đánh giá phương trình cho từng tham số a. Để bắt đầu, kết quả của f(x) là prediction (dự đoán) của chúng ta. Gọi y là label (nhãn), có nghĩa là đầu ra thực sự và mong muốn.
Với f(x) và y, chúng ta có thể xác định loss function (hàm mất mát). Một hàm mất mát chỉ đơn giản là sự khác biệt giữa các dự đoán và nhãn của chúng ta, | f (x) – y |. Sử dụng hàm này, sau đó chúng ta có thể đánh giá các tham số khác nhau cho cho mô hình. Quá trình chọn ra tham số tốt nhất cho phương trình được gọi là training (huấn luyện). Nếu chúng ta có một vài tham số tiềm năng, chúng ta chỉ cần thử từng tham số vào hàm: | f (x) – y | = | ax – y| , và chọn một phần tử có loss nhỏ nhất!
Tuy nhiên, hầu hết các vấn đề không đơn giản vậy. Điều gì xảy ra nếu có vô số các tham số khác nhau? Nghĩ sao với tất cả các giá trị thập phân từ 0 đến 1? Giữa 0 và dương vô cùng? Điều này đưa chúng ta đến chủ đề tiếp theo: Abstraction (trừu tượng) trong Machine Learning. Chúng ta sẽ thảo luận về các khía cạnh khác nhau của Machine Learning, để sắp xếp kiến thức của bạn theo các phần dữ liệu, mô hình, mục tiêu và phương pháp giải quyết. Ngoài việc học đúng tham số, còn có rất nhiều thách thức khác: làm thế nào để chúng ta xử lý một vấn đề phức tạp như điều khiển con robot? Điều khiển một chiếc xe tự lái? Việc huấn luyện một giao thức nhận diện khuôn mặt có nghĩa là gì? Phần tiếp theo sẽ giúp bạn sắp xếp câu trả lời cho những câu hỏi này.
Abstraction trong Machine Learning
4 chủ đề cơ bản trong Machine Learning
Có vô số chủ đề trong Machine Learning ở nhiều cấp độ khác nhau. Để hiểu rõ hơn về nơi mỗi mảnh ghép thuộc về trong bức tranh lớn hơn, bạn hãy cùng chúng tôi xem xét các Abstraction sau đây. Những Abstraction này phân chia những chủ đề chúng ta thảo luận ra các chủ đề nhỏ về Machine Learning, và chúng sẽ giúp bạn dễ dàng hơn trong việc kết luận các chủ đề. Các chủ đề này được phân loại bởi nghiên cứu của Giáo sư Jonathan Shewchuck tại UC Berkeley:
Ứng dụng và dữ liệu
Xem xét các Input có thể và Output cho vấn đề mong muốn.
– Câu hỏi: Mục tiêu của bạn là gì? Cấu trúc dữ liệu như thế nào? Có nhãn không? Có hợp lý không khi chúng ta trích xuất Output từ các Input được cung cấp?
– Ví dụ: Mục tiêu là phân loại hình ảnh của các chữ số viết tay. Input là một hình ảnh của một chữ số viết tay. Output là một chữ số đó.
Mô hình
Xác định loại hàm đang xem xét.
– Câu hỏi: Các hàm tuyến tính có thích đáng không? Hàm bậc hai? Hàm đa thức? Những loại mô hình nào chúng ta quan tâm? Mạng nơ-ron nhân tạo (neural networks) hay hồi quy logistic có thích hợp?
– Ví dụ: Hồi quy tuyến tính
Vấn đề tối ưu hóa
Xây dựng thể thức mục tiêu cụ thể trong toán học.
– Câu hỏi: Làm thế nào để chúng ta xác định được những mất mát? Và xác định một cách chính xác? Chúng ta có nên áp dụng hình phạt bổ sung để áp dụng lên thuật toán của chúng ta? Có sự mất cân bằng trong dữ liệu khách quan chúng ta cần xem xét?
– Ví dụ: Tìm x bằng cách tối giản | Ax-b | ^ 2
Thuật toán tối ưu hóa
Xác định cách bạn sẽ giải quyết vấn đề tối ưu hóa.
– Câu hỏi: Chúng ta có thể giải một phương trình bằng tay không? Chúng ta có cần một thuật toán lặp không? Chúng ta có thể chuyển đổi vấn đề này thành một vấn đề tương đương nhưng dễ giải quyết hơn và giải quyết nó không?
– Ví dụ: Lấy đạo hàm của hàm. Đặt nó về 0. Giải quyết cho tham số tối ưu.
Phân tích các chủ đề trong Machine Learning
Abstraction 1: Dữ liệu
Trong thực tế, thu thập, quản lý và lưu trữ dữ liệu chiếm 90% của trận chiến. Dữ liệu chứa các mẫu trong đó mỗi mẫu là một nhận thức cụ thể về Input của chúng ta.
Ví dụ, Input là hình ảnh của những chú chó: Mẫu đầu tiên cụ thể là hình ảnh của Maxie, một chú chó lai giữa chó núi Bern với giống chó Chow Chow. Mẫu thứ hai là hình ảnh của Charlie, một chú chó Corgi con.
Trong mô hình đào tạo, điều quan trọng là xử lý dữ liệu đúng cách. Điều này có nghĩa là tách dữ liệu của chúng ta cho phù hợp và không tò mò biết trước tại bất kỳ bộ dữ liệu nào. Nói chung, dữ liệu của chúng ta được chia thành ba phần:
- Tệp huấn luyện
Đây là tập dữ liệu bạn luyện tập mô hình trên đó. Mô hình có thể thấy tập này hàng trăm lần.
- Tệp xác định
Đây là tập dữ liệu bạn đánh giá mô hình của mình, để đánh giá độ chính xác và điều chỉnh phương trình hoặc phương pháp của bạn cho phù hợp.
- Tệp thử nghiệm
Đây là bạn đánh giá độ chính xác tập dữ liệu, một lần duy nhất. Chạy tập thử nghiệm trước thời hạn có thể gây quá tải với tệp dữ liệu, vì vậy chỉ chạy một lần. Chúng ta sẽ thảo luận về khái niệm “Overfitting” chi tiết dưới đây.
Abstraction 2: Mô hình
Phương thức Machine Learning được chia thành hai phần sau:
Học có giám sát (Supervised Learning)
Trong học có giám sát, thuật toán của chúng ta có quyền truy cập vào dữ liệu được dán nhãn. Tuy nhiên, chúng ta khám phá hai lớp vấn đề sau:
- Phân loại (Classification)
Xác định lớp k nào {C_1, C_2, … C_k} mà mỗi sample thuộc về.
Ví dụ: “Đây là giống chó nào?”
Chúng có thể là một trong số {“Corgi”, “chó núi Bern”, “Chow Chow” …}
- Hồi quy (Regression)
Xác định giá trị thực Output (thường là xác suất)
Ví dụ: “Xác suất bệnh nhân này mắc bệnh u nguyên bào thần kinh (ung thư mắt) là bao nhiêu?”
Học không có giám sát (Unsupervised Learning)
Trong học không có giám sát, thuật toán của chúng ta không có quyền truy cập vào nhãn và chúng ta khám phá các lớp vấn đề sau:
- Phân cụm (Clustering)
Phân các mẫu cụm thành k cụm.
Ví dụ: “Những chuỗi DNA nào giống nhau nhất?”. Chúng ta không có label cho các cụm kết quả.
- Giảm chiều dữ liệu (Dimensionality reduction)
Giảm số lượng các tính năng duy nhất (độc lập tuyến tính) mà chúng ta xem xét.
Ví dụ: “Những đặc điểm chung của những khuôn mặt này là gì?”
Abstraction 3: Mục tiêu tối ưu hóa
Trước khi thảo luận về các mục tiêu và thuật toán tối ưu hóa, chúng ta sẽ cần một ví dụ để bàn luận. Bình phương cực tiểu (least square) là ví dụ điển hình. Chúng ta sẽ hạn chế sự chú ý của chúng ta vào một công thức cụ thể của các bình phương cực tiểu: Chúng ta hãy quay trở lại vấn đề lý thuyết như trên trường giảng dạy để liên tưởng đến các quan điểm:
Hãy nhớ lại phương trình đường thẳng: y = mx + b
Giả sử chúng ta có một đường thẳng như dưới đây, là mô hình thực cơ bản.
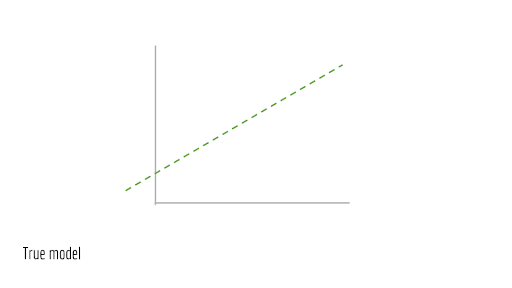
Bây giờ, hãy lấy điểm mẫu trên đường này.
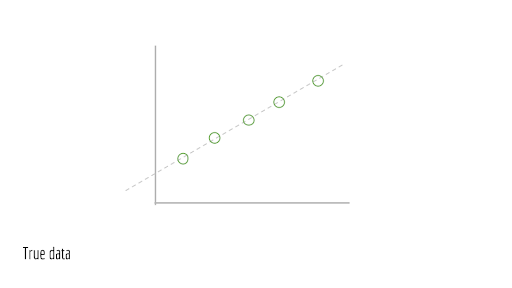
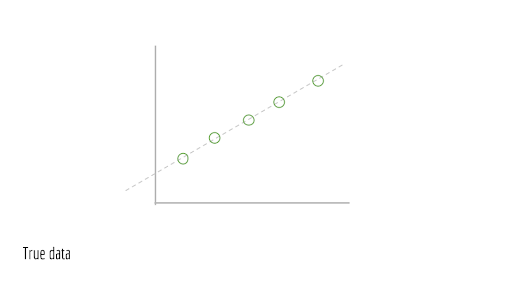
Đối với mỗi điểm, hãy đẩy nhẹ chúng một chút. Nói cách khác, hãy gây nhiễu, sự nhiễu loạn ngẫu nhiên. Nhiễu này là do đặt trong các quá trình thế giới thực. Điều này có thể là do sự thiếu chính xác trong các phép đo, nén có tổn hao, v.v.
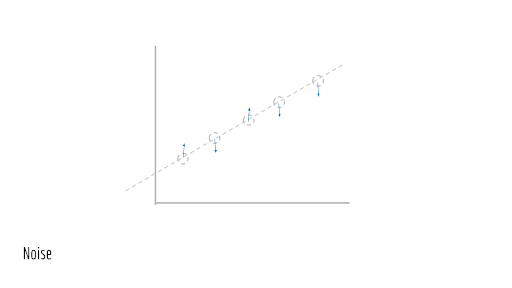
Điều này cho chúng ta Observed Data (dữ liệu quan trắc). Chúng ta sẽ gọi những điểm này là (x_1, y_1), (x_2, y_2), (x_3, y_3) …. Đây là Training Data (dữ liệu huấn luyện) chúng ta được cung cấp thực hiện. Chúng ta không có quyền truy cập vào đường cơ sở đã tạo ra dữ liệu này (đường màu xanh lam ban đầu).
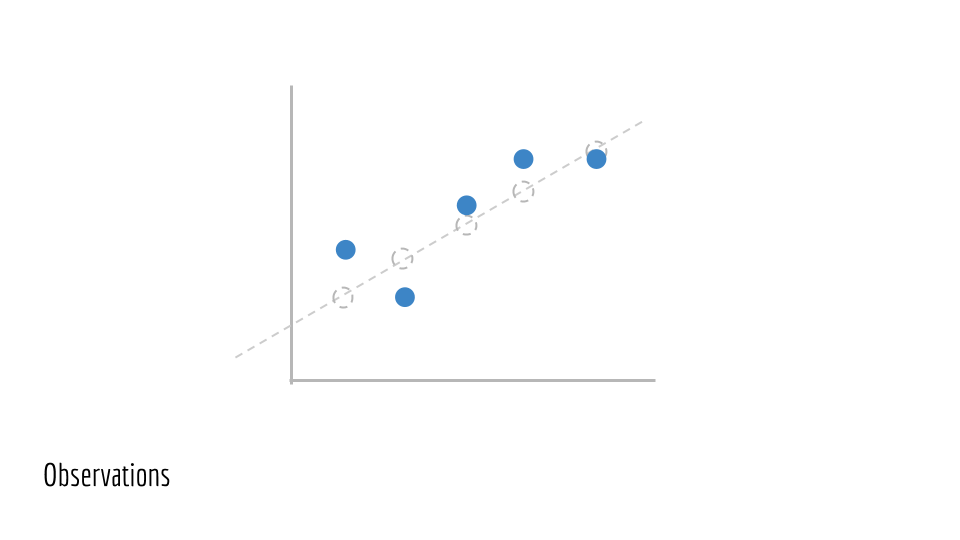
Chúng ta sẽ ước tính các tham số được đưa ra trên đường thẳng. Trong trường hợp này, các tham số là m và b. Điều này cho chúng ta một đường giả định, đường vẽ màu xanh dương bên dưới.

Chúng ta muốn đánh giá đường màu xanh dương để xem độ chính xác đến mức nào. Bắt đầu sử dụng a và b để ước tính y. Chúng ta tính toán một tập các giá trị của ŷ.
ŷ_i = m * x_i + b
Giả định là ŷ_i lỗi, và y_i đúng chỉ đơn giản là
(ŷ_i−y_i^2
Tổng lỗi sau đó là tổng của các bình phương, trên tất cả các mẫu. Điều này gây ra sự mất mát.
∑(ŷ_i−y_i)^2
Một cách trực quan, đây là khoảng cách dọc giữa các điểm quan sát và đường giả định.
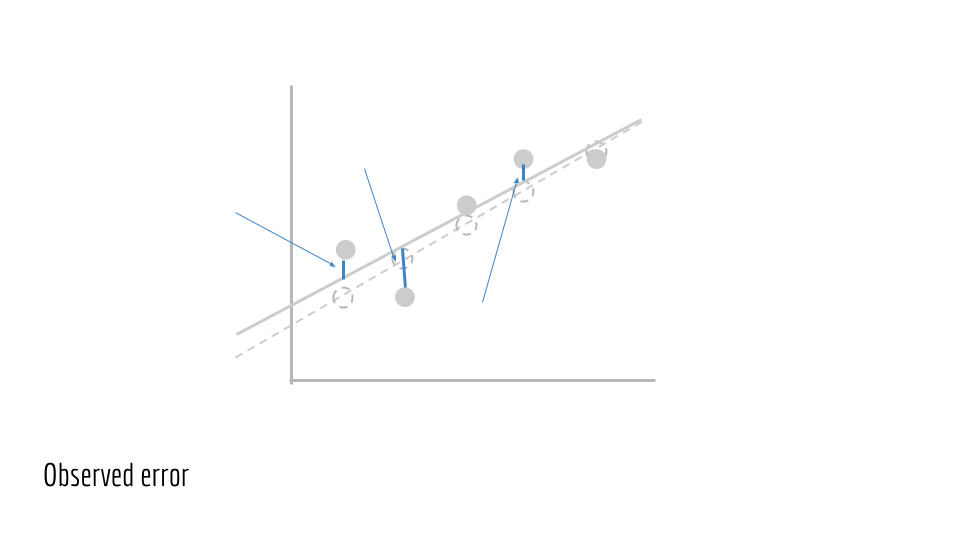
Gán ŷ_i từ phía trên, sau đó chúng ta có tổng số lỗi về các biến m và b như sau
∑(m * x_i + b − y_i)^2
Cuối cùng, chúng ta muốn giảm thiểu số lượng này. Điều này mang lại chức năng mục tiêu của chúng ta, Abstraction 3 từ danh sách Abstraction của chúng ta ở trên.
min_{m, b} ∑(a * x_i + b−y_i)^2
Mục tiêu của các phương trình trên trong toán học là giảm thiểu mất mát bằng cách thay đổi giá trị của a và b. Mục đích của phần này là để thúc đẩy phù hợp với một đường phù hợp nhất, một trường hợp đặc biệt của bình phương nhỏ nhất. Ngoài ra, chúng cho thấy mục tiêu bình phương nhỏ nhất. Tiếp theo, chúng ta cần giải quyết mục tiêu này.
Abstraction 4: Thuật toán tối ưu hóa
Làm thế nào để tối ưu hóa thuật toán? Lấy đạo hàm đối với m, đặt thành 0 và giải. Sau khi giải, ta thu được nghiệm giải tích. Quá trình giải một nghiệm giải tích chính là thuật toán tối ưu hóa, Abstraction thứ tư và cuối cùng trong danh sách Abstraction của chúng ta.
Lưu ý: Phần quan trọng của phần này là thông báo cho bạn rằng các bình phương nhỏ nhất có nghiệm dạng đóng, nghĩa là giải pháp tối ưu cho vấn đề của chúng ta có thể được tính toán một cách rõ ràng. Để hiểu tại sao điều này là quan trọng, chúng ta cần kiểm tra một vấn đề mà không có nghiệm dạng đóng. Ví dụ: chúng ta không bao giờ có thể giải x = logx cho logarit cơ sở 10 tiêu chuẩn. Hãy thử vẽ đồ thị hai đường này và chúng ta thấy rằng chúng không bao giờ giao nhau. Trong trường hợp đó, chúng ta không có nghiệm dạng đóng. Mặt khác, các bình phương nhỏ nhất thông thường có dạng đóng – đó là tin tốt. Đối với bất kỳ vấn đề nào giảm đến bình phương tối thiểu, sau đó chúng ta có thể tính toán giải pháp tối ưu, dựa trên dữ liệu và giả định của chúng ta.
Kiến thức cơ bản cần nắm vững khi ứng dụng Machine Learning
Trước khi nghiên cứu thêm các phương thức, cần phải hiểu về sự phát triển của Machine Learning. Những điều này sẽ chi phối nghiên cứu ban đầu về Machine Learning:
Bias-variance tradeoff (phương sai – độ lệch)
– Bias: Độ lệch
– Variance: Phương sai
Một trong những lỗi ước lượng tham số Machine Learning là Overfitting (mô hình quá khớp), trong đó một mô hình rất phù hợp với Training Data (tập huấn luyện). Trong giới hạn, mô hình quá khớp sẽ ghi nhớ dữ liệu. Điều này có thể có nghĩa là nếu một người làm tốt bài kiểm tra A, người ta sẽ lặp lại mọi chi tiết cho bài kiểm tra B.
Một lỗi nữa có liên quan nhưng ít phổ biến hơn là Underfitting (mô hình chưa khớp), trong đó mô hình không đủ hàm ý để nắm rõ tất cả các thông tin quan trọng trong dữ liệu. Điều này có thể có nghĩa là người ta chỉ nhìn vào điểm bài tập về nhà để dự đoán điểm thi, bỏ qua ảnh hưởng của việc đọc ghi chú, quá trình làm bài kiểm tra và nhiều yếu tố khác. Mục tiêu của chúng ta là xây dựng một mô hình khái quát hóa cho các ví dụ mới trong khi vẫn tạo ra sự khác biệt phù hợp.
Với hai lỗi này, có nhiều cách tiếp cận để giải quyết. Một là thay đổi mục tiêu tối ưu hóa của bạn để xuất hiện thuật ngữ báo lỗi về độ phức tạp của mô hình. Một cách khác là điều chỉnh các Hyperparameter (siêu tham số) chi phối mục tiêu hoặc thuật toán của bạn, có thể tương ứng với các khái niệm, chẳng hạn như “tập huấn luyện” hoặc “xung kích”. Mối quan hệ phương sai – độ lệch cho chúng ta một cái nhìn chính xác để xác định và xử lý cả quá khớp và chưa khớp.
Hợp lý cực đại (Maximum Likelihood Estimation – MLE) + Ước lượng hợp lý cực đại (Maximum A Posteriori – MAP)
– Maximum Likelihood Estimation: Hợp lý cực đại
– Maximum A Posteriori: Ước lượng hợp lý cực đại
Giả sử chúng ta có vị kem A, B và C. Chúng ta quan sát các công thức làm kem khác nhau. Mục tiêu là dự đoán thành phẩm hương vị mỗi công thức sản xuất.
Có một cách để dự đoán hương vị dựa trên công thức là ước tính xác suất:
P(flavor|recipe)
Với xác suất này cùng một công thức mới, làm thế nào chúng ta có thể dự đoán hương vị? Áp dụng công thức, chỉ cần xem xét xác suất của từng hương vị A, B, C.
P(flavor=A|recipe) = 0.4
P(flavor=B|recipe) = 0.5
P(flavor=C|recipe) = 0.1
Sau đó, chọn hương vị có tỷ lệ xác suất cao nhất. Ở trên, hương vị B có xác suất cao nhất, theo công thức của chúng ta. Do đó, chúng tôi dự đoán thành công hương vị B. Quay lại với quy tắc trên trong toán học, chúng ta có:
argmax_{flavor} P(flavor|recipe) # argmax means take the flavor that corresponds to the max value
Tuy nhiên, theo ý của chúng tôi là ngược lại: tỷ lệ xác suất dựa trên công thức hương vị.
P(recipe|flavor)
Đối với Ước lượng Hợp lý Cực Đại, chúng ta đưa ra các giả định và thấy rằng hai giá trị tương xứng với nhau.
P(recipe|flavor) ~ P(flavor|recipe)
Vì chúng ta chỉ quan tâm đến lớp có xác suất tối đa P(flavor|recipe), nên chúng ta chỉ cần tìm lớp có xác suất tối đa, với giá trị tỷ lệ cân xứng P(recipe|flavor).
argmax_{flavor} P(recipe|flavor)
Hợp lý cực đại cung cấp mục tiêu trên như một cách để dự đoán, sử dụng xác suất dữ liệu được cung cấp nhãn.
Tuy nhiên, cho phép tôi thuyết phục bạn rằng nó hợp lý khi cho rằng chúng ta có (x|y). Chúng ta có thể ước tính điều này từ việc thu thập dữ liệu thực tế. Ví dụ: giả sử chúng ta muốn ước tính số lượng viên bi mỗi học sinh trong lớp mang theo, dựa trên số vịt đồ chơi mà học sinh mang theo.
Mỗi con vịt cao su là dữ liệu x và số viên bi là y. Chúng ta sẽ sử dụng dữ liệu mẫu này dưới đây.
| x | y |
|---|---|
| 1 | 2 |
| 1 | 1 |
| 1 | 2 |
| 2 | 1 |
| 2 | 2 |
| 1 | 2 |
Với mỗi giá trị y, chúng ta có thể tính ra số x, với phương trình P(x|y). Đối với phương trình đầu, P(x=1|y=1), hãy xem xét tất cả các thành tố, trong đó y=1. Với phương trình 2, và chỉ một trong số chúng có x=1. Do đó, P(x=1|y=1) = 1⁄2. Chúng ta có thể lặp lại điều này với tất cả các giá trị của x và y.
P(x=1|y=1) = 1/2
P(x=2|y=1) = 1/2
P(x=1|y=2) = 3/4
P(x=2|y=2) = ¼
Các số nguyên tố (Featurizations), Chính quy hóa (Regularization)
Bình phương nhỏ nhất vẽ đường phù hợp nhất cho chúng ta. Lưu ý rằng bình phương nhỏ nhất có thể vừa với mô hình bất cứ mẫu là tuyến tính với đầu vào x và đầu ra y.
Gọi m = 1. Chúng ta có phương trình sau:
y = x + b
Tuy nhiên, điều gì sẽ xảy ra nếu dữ liệu không theo một đường thẳng? Cụ thể, hãy xem xét một tập dữ liệu được lấy mẫu dọc theo một vòng tròn. Hãy nhớ rằng phương trình của một đường tròn là:
x^2 + y^2 = r^2
Bình phương nhỏ nhất liệu có phù hợp trong phương trình này? Trong trường hợp này là không. Phương trình không tuyến tính trong đầu vào x và đầu ra y. Thay vào đó, phương trình trên là bậc hai của x và y. Tuy nhiên, hóa ra chúng ta vẫn có thể sử dụng bình phương nhỏ nhất, chỉ với một sửa đổi.
Hãy xem xét những phương trình sau: nếu đầu vào của chúng ta là x_ = x^2 và y_ = y^2 thì sao? Sau đó, phương trình chúng ta đang cố gắng tìm hiểu là phương trình sau.
x_ + y_ = r^2
Đây có phải là tuyến tính trong đầu vào x_ và đầu ra y_ của phương trình không? Đúng là như vậy. Lưu ý sự tinh tế. Phương trình hiện tại vẫn là bậc hai theo x, y nhưng nó là tuyến tính theo x_, y_. Điều này có nghĩa là bình phương nhỏ nhất có thể vừa với dữ liệu nếu chúng ta bình phương x^2 và y^ 2 trước khi tạo bình phương nhỏ nhất.
Tổng quát hơn, chúng ta có thể sử dụng bất kỳ số nguyên tố phi tuyến tính nào để áp dụng bình phương nhỏ nhất cho các nhãn không tuyến tính trong các tính năng. Đây là một công cụ khá mạnh mẽ, được gọi là số nguyên tố.
Tuy nhiên, số nguyên tố còn đưa đến các mô hình phức tạp hơn. Chính quy hóa thì cho phép chúng ta xử lý sự phức tạp của mô hình, đảm bảo rằng chúng ta không quá khớp với tệp huấn luyện.
Kết Luận
Trong bài viết này, bạn đã chạm vào các chủ đề chính trong các nguyên tắc cơ bản của Machine Learning. Sử dụng các trực quan ở trên, bây giờ bạn có một framework để thảo luận về các vấn đề và giải pháp Machine Learning. Sử dụng các chủ đề cơ bản ở trên, giờ đây bạn cũng đúc rút một số khái niệm tinh túy để tìm hiểu, các công cụ cần thiết để đánh giá rủi ro và các mối quan tâm khác trong ứng dụng Machine Learning.









